Question

The gas mileage M (in mi/gal) of a car is given as a function of speed v (in mph); M (s) = - 1/28 v^2 + 4y - 80 At what driving speed will this vehicle perform with the best gas mileage? What is the vehicle's gas mileage at that speed?

Answer 1

32 mi/gal

Step-by-step explanation:

`M= -(1)/(28)v^(2)+4v-80` .... (1)

For best mileage, first find the derivative of mileage function with respect to v.

`(dM)/(dv)=-(2)/(28)v+4`

Put it equal to zero.

`(1)/(14)v = 4[/tex}</p><p>v = 56 mph</p><p>Put v = 56 in equation (1)</p><p>[tex]M= -(1)/(28)* 56^(2)+4* 56-80`

M = 32 mi/gal

Answer 2

V = 56 mph.

The mileage of vehicle is 32 mi/gal

Step-by-step explanation:

Given that

M (s) = - 1/28 v^2 + 4y - 80

But in the above equation on the place of y it should be V(velocity).

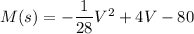`M(s)=-(1)/(28)V^2+4V-80` ---------1

We know that if we want to maximize the function then we differentiate that function .

So

`(dM)/(dV)=-2* (1)/(28)V+4`

`(dM)/(dV)=- (1)/(14)V+4`

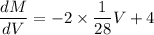
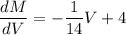
Foe maximum condition

`(dM)/(dV)=0`

`-(1)/(14)V+4=0`

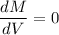
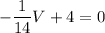
So

V= 4 x 14

V = 56 mph.

So the speed of vehicle at best mileage is 56 mph.

Now by putting the value of V in the first equation

`M(s)=-(1)/(28)V^2+4V-80`

`M(s)=-(1)/(28)* 56^2+4* 56-80`

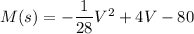
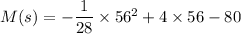
M(s) = 32

So the mileage of vehicle is 32 mi/gal