Answer:
V = 56 mph.
The mileage of vehicle is 32 mi/gal
Step-by-step explanation:
Given that
M (s) = - 1/28 v^2 + 4y - 80
But in the above equation on the place of y it should be V(velocity).
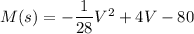 ---------1
---------1
We know that if we want to maximize the function then we differentiate that function .
So

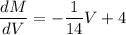
Foe maximum condition
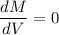
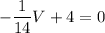
So
V= 4 x 14
V = 56 mph.
So the speed of vehicle at best mileage is 56 mph.
Now by putting the value of V in the first equation
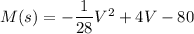
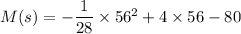
M(s) = 32
So the mileage of vehicle is 32 mi/gal