Answer:
The standard deviation of weight for this species of cockroaches is 4.62.
Explanation:
Given : A different species of cockroach has weights that are approximately Normally distributed with a mean of 50 grams. After measuring the weights of many of these cockroaches, a lab assistant reports that 14% of the cockroaches weigh more than 55 grams.
To find : What is the approximate standard deviation of weight for this species of cockroaches?
Solution :
We have given,
Mean

The sample mean x=55
A lab assistant reports that 14% of the cockroaches weigh more than 55 grams.
i.e. P(X>55)=14%=0.14
The total probability needs to sum up to 1,


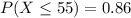
The z-score value of 0.86 using z-score table is z=1.08.
Applying z-score formula,

Where,
 is standard deviation
is standard deviation
Substitute the values,

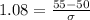
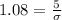
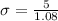
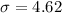
The standard deviation of weight for this species of cockroaches is 4.62.