Question

Julia owns a coffee shop. She experimented with mixing City Roast Colombian coffee that costs $7.80 per pound with French Roast Colombian coffee that costs $8.10 per pound to make a 20-pound blend. Her blend should cost her $7.92 per pound. How much of each type of coffee should she buy?

Answer 1

Explanation:

x = City Roast Colombian coffee

y = French Roast Colombian coffee

x + y = 20

Answer 2

Answer: They should buy 12 pounds of City Roast and 8 pounds of French Roast.

Explanation:

Let x be the weight of City Roast colombian coffee.

Let y be the weight of French Roast Colombian coffee.

Weight of blend = 20 pounds

So, our equation becomes

`x+y=20--------------(1)`

Cost of per pound of City Roast = $7.80

Cost of per pound of French Roast = $8.10

Cost of blend = $7.92

So, our equation becomes,

`7.80x+8.10x=7.92* 20\\\\7.8x+8.1y=158.4--------(2)`

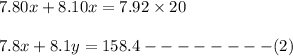
From Eq(1), we get that

`x=20-y`

Put this in Eq(2), we get that

`7.8(20-y)+8.10y=158.4\\\\156-7.8y+8.10y=158.4\\\\0.3y=158.4-156\\\\0.3y=2.4\\\\y=(2.4)/(0.3)\\\\y=8`

`x=20-y\\\\x=20-8\\\\x=12`

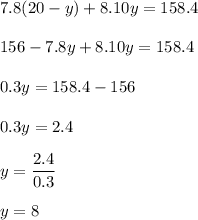
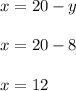
Hence, they should buy 12 pounds of City Roast and 8 pounds of French Roast.