Question

The slope of the line tangent to the curve 3x^2-2xy+y^2=11 at the point (1, -2) is ?

Answer 1

5/3

Explanation:

The previous explanation was incorrect because they forgot to differentiate the other side of the equation (11), which would actually become 0, and make the answer 5/3

Answer 2

Given :

A curve : 3x² - 2xy + y² = 11

To Find :

The slope of the line tangent to the curve 3x^2-2xy+y^2=11 at the point (1, -2).

Solution :

Differentiating given curve w.r.t x is :

6x - ( 2y + 2xy' ) + 2yy' = 11

Putting the point ( 1, -2) in above equation, we get :

6 - ( 2(-2) + 2y' ) - 4y' = 11

6 - ( -4 + 2y' ) - 4y' = 11

10 - 6y' = 11

6y' = -1

`y' =(-1)/(6)`

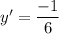
Therefore, the slope of the line tangent to the given point is
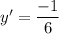`y' =(-1)/(6)` .