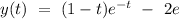Answer:
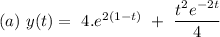
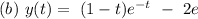
Explanation:
(a)
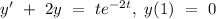
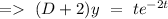
To find the complementary function
D+2 = 0
=> D = -2
So, the complementary function can by given by
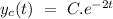
Now, to find particular integral
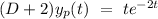
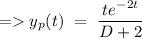
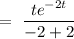
= not defined
So,
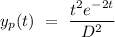
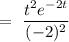
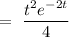
So, complete solution can be given by
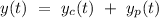
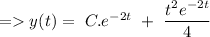
As given in question
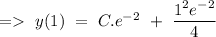
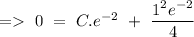
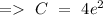
Hence, the complete solution can be give by
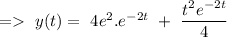
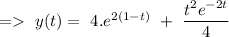
(b)
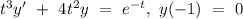
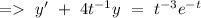
Integrating factor can be given by
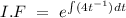
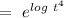
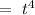
Now , the solution of the given differential equation can be given by
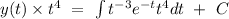
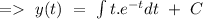
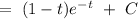
According to question
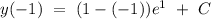

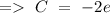
Now, the complete solution of the given differential equation cab be given by