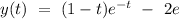Question

Find the solution of the given initial value problem:

(a) y' + 2y = te^{-2t}, y(1) = 0

(b) t^{3}y' + 4t^{2}y = e^{-t}, y(-1) = 0

Answer 1

a.
`y(t)=(t^2e^(-2t))/(2)-(1)/(2)e^(-2t)`

b.
`y=-t^(-3)e^(-t)-t^(-4)e^(-t)`

Explanation:

We are given that

a.
`y'+2y=te^(-2t),y(1)=0`

Compare with
`y'+P(t)y=Q(t)`

We have P(t)=2,Q(t)=
`te^(-2t)`

Integration factor=
`\int e^(2dt)=e^(2t)`

`y\cdot I.F=\int Q(t)\cdot I.F dt+C`

Substitute the values then, we get

`y\cdot e^(2t)=\int te^(-2t)\cdot e^(2t) dt+C`

`y\cdot e^(2t)=\int tdt+C`

`ye^(2t)=(t^2)/(2)+C`

Substitute the values x=1 and y=0

Then, we get
`0\cdot e^2=(1)/(2)+C`

`C=-(1)/(2)`

Substitute the value in the given function

`ye^(2t)=(t^2)/(2)-(1)/(2)`

`y=(t^2)/(2)e^(-2t)-(1)/(2)e^(-2t)`

Hence,
`y(t)=(t^2e^(-2t))/(2)-(1)/(2)e^(-2t)`

b.
`t^3y'+4t^2y=e^(-t),y(-1)=0`

`y'+(4)/(t)y=(e^(-t))/(t^3)`

`P(t)=(4)/(t),Q(t)=(e^(-t))/(t^3)`

I.F=
`\int e^{(4)/(t)dt}=e^(4lnt)=e^(lnt^4)=t^4`

`y\cdot \frac{t^4}=\int e^(-t)(t^4)/(t^3) dt+C`

`y\cdot t^4=\int te^(-t)dt+C`

`yt^4=-te^(-t)+\int e^(-t) dt+C`

`u\cdot v dt=u\int vdt-\int ((du)/(dt)\cdot \int vdt)dt`

`yt^4=-te^(-t)-e^(-t)+C`

Substitute the values x=-1,y=0 then, we get

`0=-(-1)e-e+C`

`C+e-e=0`

C=0

Substitute the value of C then we get

`yt^4=-te^(-t)-e^(-t)`

`y=-t^(-3)e^(-t)-t^(-4)e^(-t)`

Answer 2

`(a)\ y(t) =\ 4.e^(2(1-t))\ +\ (t^2e^(-2t))/(4)`

`(b)\ y(t)=\ (1-t)e^(-t)\ -\ 2e`

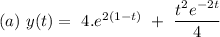
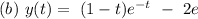
Explanation:

(a)
`y'\ +\ 2y\ =\ te^(-2t),\ y(1)\ =\ 0`

`=>\ (D+2)y\ =\ te^(-2t)`

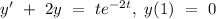
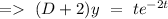
To find the complementary function

D+2 = 0

=> D = -2

So, the complementary function can by given by

`y_c(t)\ =\ C.e^(-2t)`

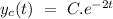
Now, to find particular integral

`(D+2)y_p(t)\ =\ te^(-2t)`

`=>y_p(t)\ =\ ( te^(-2t))/(D+2)`

`=\ ( te^(-2t))/(-2+2)`

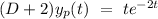
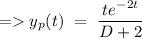
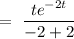
= not defined

So,

`y_p(t)\ =\ ( t^2e^(-2t))/(D^2)`

`=\ (t^2e^(-2t))/((-2)^2)`

`=\ (t^2e^(-2t))/(4)`

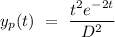
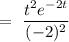
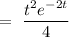
So, complete solution can be given by

`y(t)\ =\ y_c(t)\ +\ y_p(t)`

`=> y(t) =\ C.e^(-2t)\ +\ (t^2e^(-2t))/(4)`

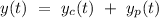
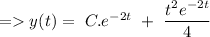
As given in question

`=>\ y(1)\ =\ C.e^(-2)\ +\ (1^2e^(-2))/(4)`

`=>\ 0\ =\ C.e^(-2)\ +\ (1^2e^(-2))/(4)`

`=>\ C\ =\ 4e^2`

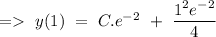
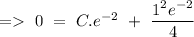
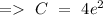
Hence, the complete solution can be give by

`=>\ y(t) =\ 4e^2.e^(-2t)\ +\ (t^2e^(-2t))/(4)`

`=>\ y(t) =\ 4.e^(2(1-t))\ +\ (t^2e^(-2t))/(4)`

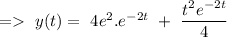
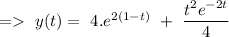
(b)
`t^(3)y'\ +\ 4t^(2)y\ =\ e^(-t),\ y(-1)\ =\ 0`

`=>\ y'\ +\ 4t^(-1)y\ =\ t^(-3)e^(-t)`

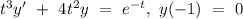
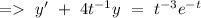
Integrating factor can be given by

`I.F\ =\ e^{\int (4t^(-1))dt}`

`=\ e^(log\ t^4)`

`=\ t^4`

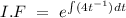
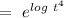
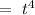
Now , the solution of the given differential equation can be given by

`y(t)* t^4\ =\ \int t^(-3)e^(-t)t^4dt\ +\ C`

`=>\ y(t)\ =\ \int t.e^(-t)dt\ +\ C`

`=\ (1-t)e^(-t)\ +\ C`

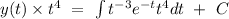
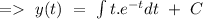
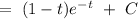
According to question

`y(-1)\ =\ (1-(-1))e^1\ +\ C`

`=>\ 0\ =\ 2e\ +\ C`

`=>\ C\ =\ -2e`

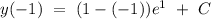
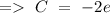
Now, the complete solution of the given differential equation cab be given by

`y(t)\ =\ (1-t)e^(-t)\ -\ 2e`