Answer:
Option 1 -
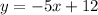
Explanation:
Given : A given line has the equation
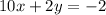
To find : What is the equation, in slope-intercept form, of the line that is parallel to the given line and passes through the point (0, 12)?
Solution :
The slope intercept form is
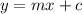
where, m is the slope and c is the y-intercept.
Writing given equation in slope intercept form,
Equation
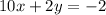
Take x to another side,

Divide both side by 2,
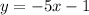
The slope intercept form of the equation is
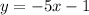
Where, m=-5 is the slope and c=-1 is the y-intercept.
When two lines are parallel their slopes are equal i.e.
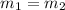
Let the equation be
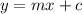
As lines are parallel then m=-5
We have given lines passes through point (0,12).
Substitute in equation,


Substitute back in equation,
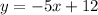
Therefore, The required equation is
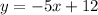
So, Option 1 is correct.