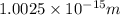Question

What is the De Broglie wavelength of an electron under 150 V acceleration?

Answer 1

Answer : The De Broglie wavelength of an electron is
`1.0025* 10^(-15)m`

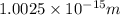
Explanation :

According to de-Broglie, the expression for wavelength is,

`\lambda=(h)/(mv)`

The formula used for kinetic energy is,

`K.E=(1)/(2)mv^2`

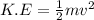
The kinetic energy in terms of momentum will be,

p = m v

`K.E=(1)/(2)mv^2=(p^2)/(2m)`

or,

`p=√(2mK.E)=mv`

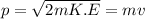
As we know that,

`K.E=q* V`

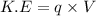
where,

'q' is charge of electron
`(1.6* 10^(-9)C)` and 'V' is potential difference.

So,
`p=√(2m* q* V)=mv`

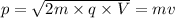
The de Broglie wavelength of the electron will be:

`\lambda=(h)/(√(2m* q* V))` .........(1)

where,

h = Planck's constant =
`6.626* 10^(-34)Js=6.626* 10^(-34)kgm^2/s`

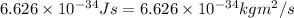
m = mass of electron =
`9.1* 10^(-31)kg`

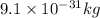
q = charge of electron =
`1.6* 10^(-9)C`

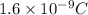
V = potential difference = 150 V

Now put all the given values in equation 1, we get:

`\lambda=\frac{6.626* 10^(-34)kgm^2/s}{\sqrt{2* (9.1* 10^(-31)kg)* (1.6* 10^(-9)C)* (150V)}}`

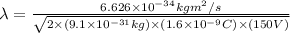
conversion used :
`(1CV=1J=1kgm^2/s^2)`

`\lambda=1.0025* 10^(-15)m`

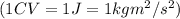
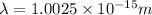
Therefore, the De Broglie wavelength of an electron is
`1.0025* 10^(-15)m`

Answer 2

0.1 nm

Step-by-step explanation

Potential deference of the electron is given as V =150 V

Mass of electron
`m=9.1* 10^(-31)`

Let the velocity of electron = v

Charge on the electron
`=1.6* 10^(-19)C`

plank's constant h =
`6.67* 10^(-34)`

According to energy conservation
`eV =(1)/(2)mv^2`

`v=\sqrt{(2eV)/(M)}=\sqrt{(2* 1.6* 10^(-19)* 150)/(9.1* 10^(-31))}=7.2627* 10^(-6)m/sec`

Now we know that De Broglie wavelength
`\lambda =(h)/(mv)=(6.67* 10^(-34))/(9.1* 10^(-31)* 7.2627*10^6 )=0.100* 10^(-9)m=0.1nm`