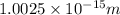Answer : The De Broglie wavelength of an electron is
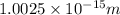
Explanation :
According to de-Broglie, the expression for wavelength is,
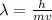
The formula used for kinetic energy is,
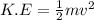
The kinetic energy in terms of momentum will be,
p = m v
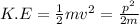
or,
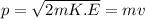
As we know that,
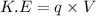
where,
'q' is charge of electron
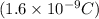 and 'V' is potential difference.
and 'V' is potential difference.
So,
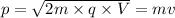
The de Broglie wavelength of the electron will be:
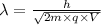 .........(1)
.........(1)
where,
h = Planck's constant =
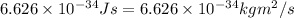
m = mass of electron =
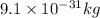
q = charge of electron =
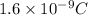
V = potential difference = 150 V
Now put all the given values in equation 1, we get:
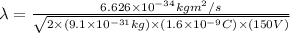
conversion used :
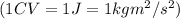
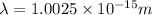
Therefore, the De Broglie wavelength of an electron is