Question

The top and bottom margins of a poster are 6 cm and the side margins are each 8 cm. If the area of printed material on the poster is fixed at 382 square centimeters, find the dimensions of the poster with the smallest area.

Answer 1

38.57 cm × 28.93 cm

Explanation:

Let x be the length of the poster ( in cm ) and y be the height ( in cm ) of the poster,

Then the area of the poster,

A = x × y

∵ The top and bottom margins of a poster are 6 cm and the side margins are each 8 cm,

Thus, the total area of the poster other than printed material = 2(6x) + 2(8y) - 4(48) ( shown in the below diagram )

= 12x + 16y - 192

We have the printed area = 382 cm²

So, the area of the poster = printed area + non printed area

= 382 + 12x + 16y - 192

= 190 + 12x + 16y

∵ Area of the poster, A = xy

⇒ xy = 190 + 12x + 16y

⇒ y(x-16) = 190 + 12x

⇒
`y=(190+12x)/(x-16)----(1)`

Area of the poster,

`A(x)=x((190+12x)/(x-16))`

`=(190x+12x^2)/(x-16)`

Differentiating with respect to x,

`A'(x)=((x-16)(190+24x)-(190x+24x^2)(1))/((x-16)^2)`

`=(12x^2-384x-3040)/((x-16)^2)`

Again differentiating with respect to x,

`y''=(12224)/((x-16)^3)`

For maxima or minima,

y'=0

`\implies (12x^2-384x-3040)/((x-16)^2)=0`

`\implies 12x^2-384x-3040=0`

`\implies x\approx 38.57\text{ or }x\approx -6.57`

Since, dimension can not be negative,

If x = 38.57,

A''(x) = positive

Hence, A(x) is minimum,

From equation (1),

`y=(190+12(38.57))/(38.57-16)=28.93`

Therefore, the required dimensions are 38.57 cm × 28.93 cm

Answer 2

The total height and width of the poster is approximately 28.93 and 38.57.

Explanation:

Consider the provided information.

Let us consider the width and length of the printed part of the poster is x and y respectively.

For better understanding refer the figure 1:

The area of the printed part is 382 cm²

Area = xy = 382

y = 382/x

Now the total height of the poster is y + 6 + 6 = y + 12

Total width of the poster is x + 8 + 8 = x + 16

Thus the total area of the poster is:

A = (x + 16)(y + 12)

Now substitute the value of y in above equation.

`A = (x+16)((382)/(x)+12)`

`A = 382+12x+(6112)/(x)+192`

`A = 12x+(6112)/(x)+574`

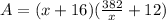
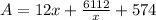
Now differentiate the above equation with respect to x.

`A' = 12-(6112)/(x^2)`

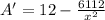
Now, substitute A'= 0 and solve for x.

`0 = 12-(6112)/(x^2)`

`12=(6112)/(x^2)`

`x^2=(6112)/(12)`

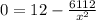
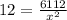
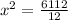
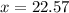`x=22.57` Ignore the negative value of x as width can't be a negative number.

Now find A''

`A'' = (2(6112))/(x^3)`

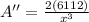
Here A" is positive for x>0 and x = 22.57 is minimum.

Use the value of x to find all the respective dimensions of the poster.

Substitute the value of x in y = 382/x

y = 382/22.57 = 16.93

The total height of the poster is y + 6 + 6 = y + 12 = 16.93 + 12 = 28.93

Total width of the poster is x + 8 + 8 = x + 16 = 22.57 + 16 = 38.57

Hence, the total height and width of the poster is approximately 28.93 and 38.57.