Answer:
Option D -1
Step-by-step explanation:
Given : Function
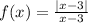
To find : What is the left-hand limit of function as approaches 3?
Solution :
Function
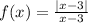
In left-hand limit,
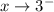
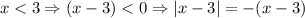
So,
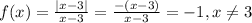
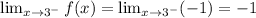
Therefore, The left-hand limit of function as approaches 3 is -1.
So, Option D is correct.