Question

The base of a regular hexagonal pyramid has sides 6 feet long and a slant height of 12 feet. What is the lateral area of the pyramid?

Answer 1

216

Explanation:

formula = 1/2 * b * h *6

formula = 1/2 * 6 * 12 * 6 = 216

Answer 2

`216\text{ feet}^2`

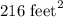
Explanation:

We have been given that the base of a regular hexagonal pyramid has sides 6 feet long and a slant height of 12 feet. We are asked to find the lateral area of the pyramid.

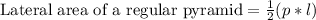`\text{Lateral area of a regular pyramid}=(1)/(2)(p*l)`, where,

p = Perimeter of base of pyramid,

l = Slant height.

Since each side of the the hexagonal base is 6 feet, so perimeter of base would be
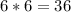`6*6=36` feet.

`\text{Lateral area of a regular hexagonal pyramid}=(1)/(2)(36* 12)`

`\text{Lateral area of a regular hexagonal pyramid}=18* 12`

`\text{Lateral area of a regular hexagonal pyramid}=216`

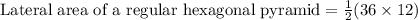
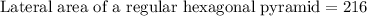
Therefore, the lateral area of hexagonal pyramid would be 216 square feet.