Answer:
-3c
Explanation:
We are given that an expression
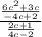
We have to find an expression which is equal to given expression
Taking common 3c from nominator and -2 from denominator in dividened and 2 common in divisor then we get

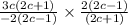
By reciprocal divisor
By canceling same factor
Then ,we get
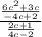
=-3c