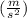Answer:
A. 2.249 hz
B. 0.45 s
C. 0.424 m/s
D. 66⁰
E. 6 m/s^2
Step-by-step explanation:
Step 1: identify the given parameters
mass of the block (m)= 0.75kg
stiffness constant (k) = 150N/m
Amplitude (A) = 3cm = 0.03m
upward velocity (v) = 2cm/s
Step 2: calculate the natural frequency (F)by applying relevant formula in S.H.M
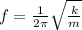
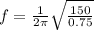
f = 2.249 hz
Step 3: calculate the period of the oscillation (T)
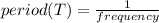

T = 0.45 s
Step 4: calculate the maximum velocity,
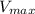

A is the amplitude of the oscilation

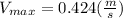
Step 5: calculate the phase angle, by applying equation in S.H.M
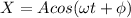
where X is the displacement; calculated below
Displacement = upward velocity X period of oscillation
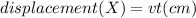
X = (2cm/s) X (0.45 s)
X = 0.9 cm = 0.009m
where
 is omega; calculated below
is omega; calculated below
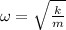
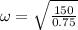
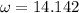
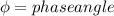
Applying displacement equation in S.H.M
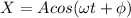
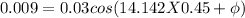
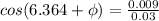
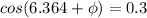
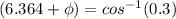
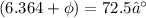

 =72.5 -6.364
=72.5 -6.364
 =66.1⁰
=66.1⁰
Phase angle,
 ≅66⁰
≅66⁰
Step 6: calculate the maximum acceleration,
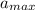
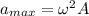
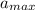 = 14.142 X 14.142 X 0.03
= 14.142 X 14.142 X 0.03
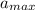 = 5.999
= 5.999
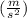
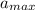 ≅ 6
≅ 6