Finding angles outside of a circle. Solve for x :))

Question

asked Dec 12, 2020 192k views

2 Answers

Tstseby · Answer 1 · 2020-12-14T00:14:32+0000

Answer:

x=6

Explanation:

So we have the difference of the intercept arcs divided by 2 is the angle formed by the two tangents there.

So we have

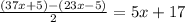
((37x+5)-(23x-5))/(2)=5x+17

Clear the fraction by multiplying both sides by 2:

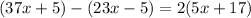
(37x+5)-(23x-5)=2(5x+17)

Distribute:

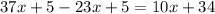
37x+5-23x+5=10x+34

Combine like terms on the left hand side:

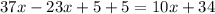
37x-23x+5+5=10x+34

Simplify:

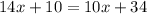
14x+10=10x+34

Subtract 10x on both sides:

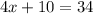
4x+10=34

Subtract 10 on both sides:

4x=24

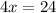
Divide both sides by 4:

x=6