Answer:
-16 cents
Explanation:
We are given that on three rolls of a single die, you will lose $19 if a 3 turns up at least once, and you will win $5 otherwise.
We are to find the expected value of the game.
P (at least one 5 in three rolls) = 1 - P (no. of 3 in three) =
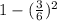 = 0.875
= 0.875
P (other results) = 1 - 0.875 = 0.125
Random game value = -19, +5
Probabilities: 0.875, 0.125
Expected game value (X) = 0.875 × (-19) + 0.125 × (5) = -16 cents
Therefore, every time you play the game, you can expect to lose 16 cents