Answer:
You need 63.66 turns.
Step-by-step explanation:
The number of turns of a magnetic field is given by the following formula:
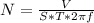
In which N is the number of turns, V is the maximum output voltage, S is the area of the rotating coil, in square meters and T is the measure of the magnetic field and f is the frequency.
In this problem, we have that:
Suppose that you wish to construct a simple ac generator having an output of 12 V maximum when rotated at 60 Hz. This means that
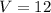 and
and
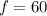 .
.
A uniform magnetic field of 0.050 T is available. This means that
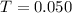 .
.
If the area of the rotating coil is 100 cm2, how many turns do you need?
This means that
 m². So:
m². So:
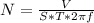
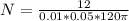
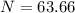
You need 63.66 turns.