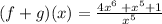ANSWER
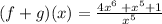
EXPLANATION
The given functions are:
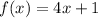
and

We now want to find
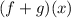
We use this property of Algebraic functions.
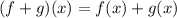
We substitute the functions to get:
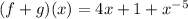
Writing as a positive index, we get:
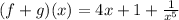
The property we used to obtain the positive index is
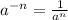
We now collect LCD to get:
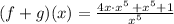
This simplifies to: