Question

Determine whether the function f(x) = 3(x − 1)4 is even or odd.

Answer 1

Other answer.

Explanation:

`f(x) = 3(x-1)^4\\ f(-x) = 3(-x-1)^4 = 3\big(-(x+1)\big)^4 = 3(x+1)^4 \\ \\ f(-x)\\eq f(x) \\ f(-x)\\eq -f(x)\\ \\ \Rightarrow \text{The function is neither odd or even}`

Answer 2

The function is neither even nor odd.

Explanation:

Given : Function
`f(x)=3(x-1)^4`

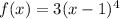
To find : Determine whether the function is even or odd ?

Solution :

Rules to determine the function is even or odd :

If f(x)=f(-x) then the function is even.

If f(x)=-f(x) then the function is odd.

Now, Test for even function

`f(x)=3(x-1)^4`

`f(-x)=3(-x-1)^4`

`f(-x)=3(-(x+1)^4`

`f(-x)=3(x+1)^4`

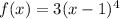
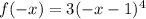
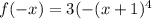
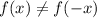`f(x)\\eq f(-x)` so function is not even.

Test for odd function,

`f(x)=3(x-1)^4`

`-f(x)=-3(x-1)^4`

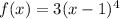
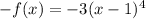
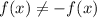`f(x)\\eq -f(x)` so function is not odd.

So, The function is neither even nor odd.