Answer:
The function is neither even nor odd.
Explanation:
Given : Function
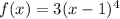
To find : Determine whether the function is even or odd ?
Solution :
Rules to determine the function is even or odd :
If f(x)=f(-x) then the function is even.
If f(x)=-f(x) then the function is odd.
Now, Test for even function
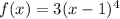
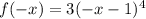
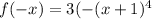
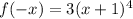
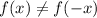 so function is not even.
so function is not even.
Test for odd function,
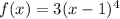
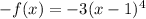
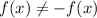 so function is not odd.
so function is not odd.
So, The function is neither even nor odd.