Answer:
the explicit formula for the geometric sequence 2,6,18,54 is
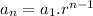
2,6,18,54
Explanation:
In the sequence given: 2,6,18,54
The common ration is 3 because
a₁ = 2
a₂= 2*3 =6
a₃ = (2*3)*3 = 2*3^2 = 18
a₄= (2*3*3)*3 =2*3^3 = 54
Here we see for a₂ 3 has power 1, for a₃ 3 has power 2 and so on.
So, the formula will be
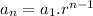
Here aₙ is the no of term.
a₁ is the first term of the sequence
and r is the common ratio among the sequence.