Question

Find the explicit formula for the geometric sequence
2,6,18,54

Answer 1

b(n)=2⋅3 ^n−1

Answer 2

the explicit formula for the geometric sequence 2,6,18,54 is
`a_(n)=a_(1).r^(n-1)`

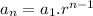
2,6,18,54

Explanation:

In the sequence given: 2,6,18,54

The common ration is 3 because

a₁ = 2

a₂= 2*3 =6

a₃ = (2*3)*3 = 2*3^2 = 18

a₄= (2*3*3)*3 =2*3^3 = 54

Here we see for a₂ 3 has power 1, for a₃ 3 has power 2 and so on.

So, the formula will be

`a_(n)=a_(1).r^(n-1)`

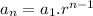
Here aₙ is the no of term.

a₁ is the first term of the sequence

and r is the common ratio among the sequence.