Answer:
The resulting function after the sequence of transformations is
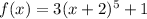
Explanation:
Given a function f(x)
- the function a*f(x) will be a vertical stretch of factor a, given a > 1
- the function f(x) + b will be the translated function vertically up b units
- the function f(x+c) will be horizontally translated function of the original by c units left
Remembering these points, we can apply the rules to
 .
.
- Strech vertically by 3 would be
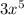
- translate up 1 unit would be
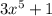
- translate left 2 units would make it

Hence the new function would be
