Question

If arc AD = 130° and arc AB = arc CD = 80°, what is the measure of ∠APD?

Answer 1

the answer is 25

Explanation:

1/2(130-80)

Answer 2

(B)

Explanation:

Given: It is given that arc AD=130° and arc AB=arc CD=80°.

To find: The measure of ∠APD.

Solution: It is given that arc AD=130°⇒m∠AOD=130° (The measure of the central angel is equal to the intercepted arc)

Also, arc AB=arc CD=80°⇒m∠AOB=m∠DOC=80° (The measure of the central angel is equal to the intercepted arc)

We know that the sum of the central angles is equal to 360°, thus

m∠AOD+m∠AOB+m∠BOC+m∠COD=360°

⇒130°+80°+m∠BOC+80°=360°

⇒290°+m∠BOC=360°

⇒m∠BOC=360°-290°

⇒m∠BOC=70°

Now, since (The measure of the central angel is equal to the intercepted arc), therefore arcBC=70°.

Also, we know that Angle Formed by Two Secants is half of the DIFFERENCE of Intercepted Arcs, therefore

`m{\angle}APD=(1)/(2) (arcAD-arBC)`

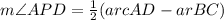
Substituting the values, we get

`m{\angle}APD=(1)/(2) (130-70)`

⇒
`m{\angle}APD=(60)/(2)`

⇒
`m{\angle}APD=30^(\circ)`

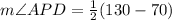
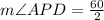
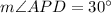
Thus, the measure of ∠APD is 30°.

Hence, option B is correct.