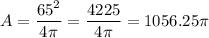Answer:
1056.25π square units
Explanation:
A few formulas an definitions which will help us:
(1)
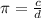 , where c is the circumference of a circle and d is its diameter
, where c is the circumference of a circle and d is its diameter
(2)
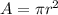 , where A is the area of a circle with radius r. To put it in terms of d, remember that a circle's diameter is simply twice its radius, or mathematically, (3)
, where A is the area of a circle with radius r. To put it in terms of d, remember that a circle's diameter is simply twice its radius, or mathematically, (3)
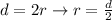 .
.
We can rearrange equation (1) to put d in terms of π and c, giving us (4)
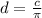 , and we can make a few substitutions in (2) using (3) and (4) to get use the area in terms of the circumference and π:
, and we can make a few substitutions in (2) using (3) and (4) to get use the area in terms of the circumference and π:
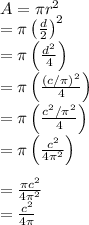
We can now substitute c for our circumference, 65, to get our answer in terms of π: