Answer:
b is correct.
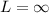
Explanation:
We are given a limit
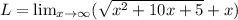
Using calculator to find the value of limit.
First we check the limit exist or not.
We have to check left and right hand limit.
For Left hand limit, LHL
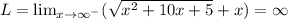
For Right hand limit, RHL
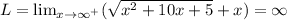
LHL=RHL=∞
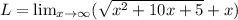
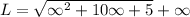
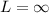
Hence, b is correct.