Question

Use a calculator to estimate the limit
Picture provided below

Answer 1

b is correct.

`L=\infty`

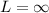
Explanation:

We are given a limit
`L=\lim_(x\rightarrow \infty)(√(x^2+10x+5)+x)`

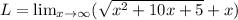
Using calculator to find the value of limit.

First we check the limit exist or not.

We have to check left and right hand limit.

For Left hand limit, LHL

`L=\lim_(x\rightarrow \infty^-)(√(x^2+10x+5)+x)=\infty`

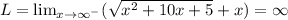
For Right hand limit, RHL

`L=\lim_(x\rightarrow \infty^+)(√(x^2+10x+5)+x)=\infty`

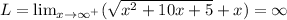
LHL=RHL=∞

`L=\lim_(x\rightarrow \infty)(√(x^2+10x+5)+x)`

`L=√(\infty^2+10\infty+5)+\infty`

`L=\infty`

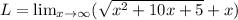
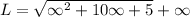
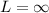
Hence, b is correct.

Answer 2

b.∞

Explanation:

Given:
`\lim_(n \to \infty) √(x^2 + 10x + 5)  + x`

This can be written as

=
`\lim_(n \to \infty) √(x^2+10x + 5)  +  \lim_(n \to \infty) x`

when applying the limit x -->∞, we get

`\lim_(n \to \infty) √(x^2 +10x + 5) =` ∞

and

`\lim_(n \to \infty) x =` = ∞

Therefore, we get

= ∞ + ∞

= ∞ [Since ∞ itself a largest number so there is no 2∞]

Answer: b.∞

Hope this will helpful.

Thank you.