Question

Which of the following expressions is not equivalent to the quotient of sqrt2(cos45° + isin45°) and sqrt2(cos315° + isin315°)?

Answer 1

Answer with explanation:

If, A complex number, Z=a + i b

then, Z can be written as,=|r| (Cos A + i Sin A), where |r|=Modulus of Complex number which is equal to

`|r|=√(a^2+b^2)\\\\A=\ Tan^(-1)((b)/(a))\\\\a=r \ Cos A\\\\b=r \ Sin A\\\\Z=|r|e^(iA)`

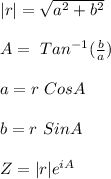
The expression which is equivalent to √2[Cos 45° +i Sin 45°] is,

`\Rightarrow √(2)( \ Cos45^(\circ) + i\ Sin 45^(\circ))\\\\\Rightarrow √(2)((1)/(√(2)) +i(1)/(√(2)) )\\\\\Rightarrow √(2)*(1+i)/(√(2))\\\\=1+ i`

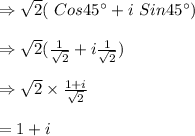
And , the expression which is equivalent to,√2[Cos 315° +i Sin 315°] is

.
`\Rightarrow √(2)( \ Cos315^(\circ) + i\ Sin 315^(\circ))\\\\\Rightarrow √(2)( \ Cos45^(\circ) - i\ Sin 45^(\circ))\\\\\Rightarrow √(2)((1)/(√(2)) -i(1)/(√(2)) )\\\\\Rightarrow √(2)*(1-i)/(√(2))\\\\=1- i`

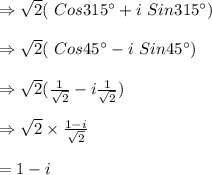
→ Cos (360°-45°)=Cos 45°

→Sin (360° -45°)= -Sin 45°

Answer 2

-i

Explanation:

Given are two complex numbers as

`z1 = √(2)  (cos 135+isin 135)</p><p>z2 = √(2) (cos 315+isin315)`

To find quotient

We can use Demoivre theorem for products and quotients here

Quotient would be equal to

`(z1)/(z2) =(√(2)(cos45+isin45) )/(√(2)(cos315+isin315) ) \\=cos (45-135)+isin(45-135)\\=cos90-isin90\\=-i`

Hence quotient = -i