Answer with explanation:
If, A complex number, Z=a + i b
then, Z can be written as,=|r| (Cos A + i Sin A), where |r|=Modulus of Complex number which is equal to
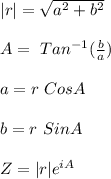
The expression which is equivalent to √2[Cos 45° +i Sin 45°] is,
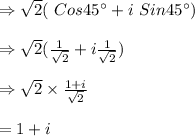
And , the expression which is equivalent to,√2[Cos 315° +i Sin 315°] is
.
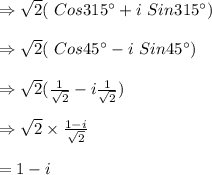
→ Cos (360°-45°)=Cos 45°
→Sin (360° -45°)= -Sin 45°