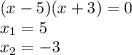Answer:
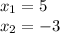
Explanation:
You have the following quadratic equation given in the problem:
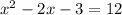
You must make the equation equal to zero, as following:
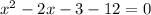
Add like terms:
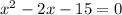
Now, to factor the equation, you must find two numbers whose sum is -2 and whose product is -15. Therefore, you have: