Answer:
0.4
Explanation:
We have been given an exponential function
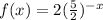 . We are asked to find the multiplicative rate of change.
. We are asked to find the multiplicative rate of change.
We will use exponent properties to solve our given problem.
Using property
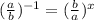 , we can rewrite our given function as:
, we can rewrite our given function as:
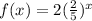
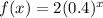
We know that an exponential function is in form
 , where,
, where,
a = Initial value,
b = Multiplicative rate of change.
Upon looking at our given function, we can see that the value of b is 0.4, therefore, the multiplicative rate of change for the given exponential function is 0.4.