Question

James is playing his favorite game at the arcade. After playing the game 3 times, he has 8 tokens remaining. He initially had 20 tokens, and the game costs the same number of tokens each time. The number tt of tokens James has is a function of gg, the number of games he plays

Answer 1

t=-4g+20

Explanation:

Answer 2

`t(g)=-4g+20`

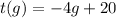
Step by step explanation:

Let g be the number of games James plays and t be the number of tokens James has.

We will write our function's formula in slope-intercept form of equation
`y=mx+b`, where,

m = Slope of line,

b = y-intercept.

We have been given that initially James has 20 tokens. This means that before playing the games James has 20 tokens or at g equals 0 t equals 20. So our y-intercept will be 20.

We are also told that after playing the game 3 times, he has 8 tokens remaining.

Let us find the slope of line using points (3,8) and (0,20).

`m=(y_2-y_1)/(x_2-x_1)`, where,

m = Slope of line,

`y_2-y_1`= Difference between two y-coordinates,

`y_2-y_1`= Difference between x-coordinates of same two y-coordinates.

Upon substituting coordinates of our given points we will get,

`m=(8-20)/(3-0)`

`m=(-12)/(3)`

`m=-4`

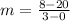
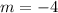
So the slope of our line will be -4.

We can see that number of remaining tokens are dependent on number games James plays, this mean that t is a function of g.

Upon substituting our values in slope-intercept form of equation we will get,

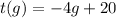`t(g)=-4g+20`, where, t(g) represents number of tokens James has left after playing g games.

Therefore, our required function will be
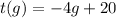`t(g)=-4g+20`.