Answer:
Option A is correct.
The table represents a direct variation because the values are proportional.
Explanation:
The direct variation says that:
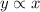
then; the equation is of the form :
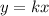 where k is the Constant of Variation.
where k is the Constant of Variation.
Consider any values of x and y from the table, to solve for k;
Let x = 10 and y = 2.5
then;
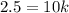
Divide both sides by 10 we have;
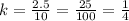
Then the equation becomes:

Therefore, the table represents a direct variation because the values are proportional.