Answer:
As, it is given that , Area of Parallelogram W X Y Z= 45 square units.
Area of Δ
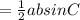
As, diagonal of parallelogram divides it into two congruent triangles and congruent triangles have equal area.
So, Area (Δ W Y Z)= Area (Δ W X Y)
Area (Δ W X Z) =Area (Δ X Y Z)
Area (Δ WYZ)
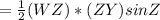
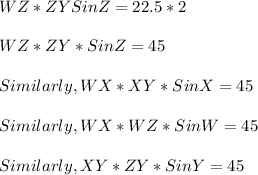
As, Opposite sides as well as Opposite angles of Parallelogram are equal.
Adding all the equation written above,
2(WZ*ZY*Sin Z )+ 2(WX*WZ*SinW)=180
2 * WZ *ZY(Sin Z +Sin W)=180
WZ *ZY(Sin Z +Sin W)=90
Consider the case when , SinZ=SinW=1, when the parallelogram turns into rectangle.
Area of Parallelogram which is rectangle =45 square units
L*B=45
Perimeter of Parallelogram = 2 * (L +B)
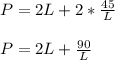
Differentiating Once w.r.t L
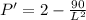
For maxima or minima
L²=45
L= 6.70 units
Gives, B= 6.72 units
Perimeter = 2 × (L +B)
= 2 × (6.70 +6.72)
=2 × 13.42
= 26.84
As, area of parallelogram is smaller than area of rectangle having same dimension.
So, Approximate perimeter of Parallelogram = 30 units.
Option C: 30 units