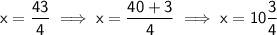Question

What is the solution to this equation?
-1/5(x+1 1/4)=-2 1/2

Answer 1

`\sf c)\ x=10(3)/(4)`

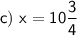
Explanation:

Given equation:

`\sf -(1)/(5)\left(x+1(3)/(4)\right)=-2(1)/(2)`

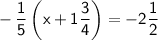
Step 1: Convert the mixed numbers into improper fractions.

`\sf -(1)/(5)\left(x+(4*1+3)/(4)\right)=-(2*2+1)/(2)\implies -(1)/(5)\left(x+(7)/(4)\right)=-(5)/(2)`

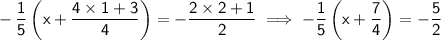
Step 2: Distribute -⅕ through the parentheses.

`\sf-(1)/(5)(x)+-(1)/(5)\left((7)/(4)\right)=-(5)/(2)\\\\\implies -(1)/(5)x-(7)/(20)=-(5)/(2)`

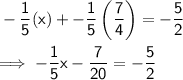
Step 3: Rewrite the equation with a common denominator of 20.

`\sf -(1*4)/(5*4)x-(7)/(20)=-(5*10)/(2*10)\\\\\implies -(4)/(20)x-(7)/(20)=-(50)/(20)`

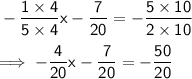
Step 4: Multiply both sides by 20.

`\sf 20\left(-(4)/(20)x\right)-20\left((7)/(20)\right)=20\left(-(50)/(20)\right)\\\\\implies -4x-7=-50`

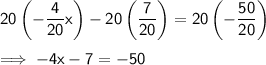
Step 5: Add 7 to both sides.

`\sf -4x-7+7=-50+7\\\\\implies -4x=-43`

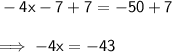
Step 6: Divide both sides by -4.

`\sf (-4x)/(-4)=(-43)/(-4)\\\\\implies x=(43)/(4)`

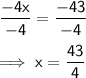
Step 7: Convert the answer back into a mixed number.

`\sf x=(43)/(4)\implies x=(40+3)/(4)\implies x=10(3)/(4)`

Answer 2

`\large\displaystyle\text{$\begin{gathered}\sf -(1)/(5)\left(x+1(3)/(4)\right)=-2(1)/(2) \end{gathered}$}`

Multiply both sides of the equation by 20, the lowest common denominator of 5,4,2.

`\large\displaystyle\text{$\begin{gathered}\sf \bf{-4\left(x+(4+3)/(4)\right)=-10(2*2+1) } \end{gathered}$}`

Add 4 and 3 to get 7.

`\large\displaystyle\text{$\begin{gathered}\sf \bf{-4\left(x+(7)/(4)\right)=-10(2*2+1) } \end{gathered}$}`

Use the distributive property to multiply −4 times x 4/7.

`\large\displaystyle\text{$\begin{gathered}\sf \bf{-4x-4*\left((7)/(4)\right)=-10(2*2+1) } \end{gathered}$}`

Multiply −4 by 4/7.

`\large\displaystyle\text{$\begin{gathered}\sf \bf{-4x-7=10(2*2+1) \ \ \to \ \ [Multiply \ 2*2] } \end{gathered}$}`

`\large\displaystyle\text{$\begin{gathered}\sf \bf{-4x-7=10(4+1) \ \ \to \ \ [Add] } \end{gathered}$}`

`\large\displaystyle\text{$\begin{gathered}\sf \bf{-4x-7=10*5 \ \ \to \ \ [Multiply] } \end{gathered}$}`

`\large\displaystyle\text{$\begin{gathered}\sf \bf{-4x-7=-50 } \end{gathered}$}`

Add 7 to both sides.

`\large\displaystyle\text{$\begin{gathered}\sf \bf{-4x=-50+7 \ \ \to \ \ [Add] } \end{gathered}$}`

`\large\displaystyle\text{$\begin{gathered}\sf \bf{-4x=-43 } \end{gathered}$}`

Divide both sides by −4.

`\large\displaystyle\text{$\begin{gathered}\sf \bf{x=(-43)/(-4) } \end{gathered}$}`

The fraction
`\bf{(-43)/(-4)}` can be simplified to
`\bf{(43)/(4)}` by removing the negative sign from the numerator and denominator.

`\large\displaystyle\text{$\begin{gathered}\sf \bf{x=(43)/(4) } \end{gathered}$}`

simplify

`\large\displaystyle\text{$\begin{gathered}\sf \bf{x=10(3)/(4) \ \ \to \ \ \ Answer } \end{gathered}$}`

{ Pisces04 }