Question

Refer to the figure below and mark all statements that are true.

A.) If the measure of θ is 1 radian, then the arc length is 2r.

B.) The ratio of arc length to r is always equal to π.

C.) If the measure of θ is 60°, then the arc length is r.

D.) If the ratio of the arc length to r is 1, then the measure of θ is 1 radian.

Answer 1

if the measure ∅ is 0.5 radians, then the arc length is r/2

Explanation:

answer

Answer 2

D is true.

Explanation:

We will use the formula for arc length (in radians) for this problem.

Arc length (s) =
`r\theta`

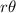
Where

• r is the radius
• 
  `\theta` is the angle in radians

A.

Arc length with
`\theta` measuring 1 and radius r is:

`s=r\theta\\s=r(1)\\s=r`

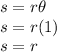
So, not 2r, as stated. So A is false.

B.

Ratio of arc length to r is:

`(ArcLength)/(r)=(r\theta)/(r)=\theta`

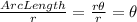
So, it's not
`\pi`, B is false.

C.

Arc length, when
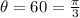`\theta=60=(\pi)/(3)` and radius is r:

`s=r\theta\\s=r((\pi)/(3))=(r\pi)/(3)`

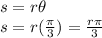
So, C is false.

D.

Setting up ratio of arc length to r as 1 and solving for
`\theta`:

`(ArcLength)/(r)=1\\(r\theta)/(r)=1\\\theta=1`

D is right.