Answer:
D is true.
Explanation:
We will use the formula for arc length (in radians) for this problem.
Arc length (s) =
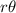
Where
- r is the radius
 is the angle in radians
is the angle in radians
A.
Arc length with
 measuring 1 and radius r is:
measuring 1 and radius r is:
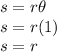
So, not 2r, as stated. So A is false.
B.
Ratio of arc length to r is:
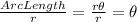
So, it's not
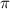 , B is false.
, B is false.
C.
Arc length, when
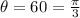 and radius is r:
and radius is r:
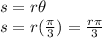
So, C is false.
D.
Setting up ratio of arc length to r as 1 and solving for
 :
:
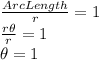
D is right.