Question

Pleaseeeee answer correctly !!!!!!!!!!!!!!! Will mark Brianliest !!!!!!!!!!!!!!!!!

Answer 1

let the third side be x

Using pythagoras theorem we get,

(58)^2 = (42)^2 + (x)^2

3364=1764+x^2

x^2=3364-1764

x^2= 1600

x=√(1,600)

x=40

Answer 2

`\pink{\sf Third \: side \: of \: the \: triangle = 40}`

Solution :

As, the given triangle is a right angled triangle,

Hence, We can use the Pythagoras' Theorem,

`\star\:{\boxed{\sf{\pink {H^(2) = B^(2) + P^(2)}}}}`

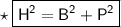
Here,

• H = Hypotenuse of triangle
• B = Base of triangle
• P = Perpendicular of triangle

In given triangle,

• Base = 42
• Hypotenuse = 58
• Perpendicular = ?

Now, by Pythagoras' theorem,

`\star\:{\boxed{\sf{\pink {H^(2) = B^(2) + P^(2)}}}}`

`\sf : \implies (58)^(2) = (42)^(2) + P^(2)`

`\sf : \implies 58 * 58 = 42 * 42 + P^(2)`

`\sf : \implies 3364 = 1764 + P^(2)`

`\sf : \implies P^(2) = 3364 - 1764`

`\sf : \implies P^(2) = 1600`

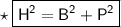
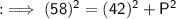
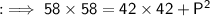
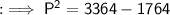
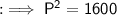
By squaring both sides :

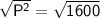
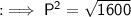
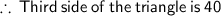
`\sf \sqrt{P^(2)} = √(1600)`

`\sf : \implies P^(2) = √(1600)`

`\sf : \implies P^(2) = \sqrt{(40)^(2)}`

`\sf : \implies P^(2) = 40`

`\pink{\sf \therefore \: Third \: side \: of \: the \: triangle \: is \: 40}`

━━━━━━━━━━━━━━━━━━━━━