Answer :

Solution :
As, the given triangle is a right angled triangle,
Hence, We can use the Pythagoras' Theorem,
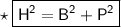
Here,
- H = Hypotenuse of triangle
- B = Base of triangle
- P = Perpendicular of triangle
In given triangle,
- Base = 42
- Hypotenuse = 58
- Perpendicular = ?
Now, by Pythagoras' theorem,
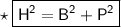
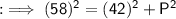
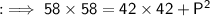
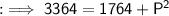
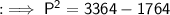
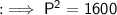
By squaring both sides :
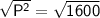
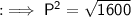
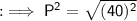
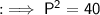
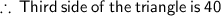
━━━━━━━━━━━━━━━━━━━━━