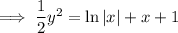Question

Use separation of variables to solve the differential equation with initial condition y(1)=-2​

Answer 1

Answer: A

Explanation:

`(dy)/(dx)=(1+x)/(xy) \\ \\ y \text{ } dy=(1+x)/(x) \text{ } dx \\ \\ y \text{ } dy= \left((1)/(x)+1 \right) \text{ } dx \\ \\ \int y \text{ } dy=\int \left((1)/(x)+1 \right) \text{ } dx \\ \\ (y^(2))/(2)=\ln \left| x \right|+x+C`

Substituting in the initial condition,

`((-2)^(2))/(2)=\ln \left|1 \right|+1+C\\\\2=1+C\\\\C=1`

So,

`\boxedx \right`

Answer 2

`\textsf{A.} \quad (1)/(2)y^2=\ln|x|+x+1`

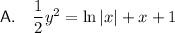
Explanation:

To solve the differential equation:

Rearrange the given equation to get all the terms containing y on the left side, and all the terms containing x on the right side:

`(dy)/(dx)=(1+x)/(xy)`

`\implies y(dy)/(dx)=(1+x)/(x)`

`\implies y\:dy=(1+x)/(x)\:dx`

`\implies y\:dy=(1)/(x)+(x)/(x)\:dx`

`\implies y\:dy=\left((1)/(x)+1\right)\:dx`

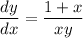
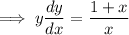
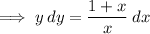
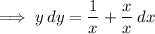
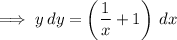
Integrate both sides:

`\displaystyle \implies \int y\:dy=\int \left((1)/(x)+1\right)\:dx`

`\implies (1)/(2)y^2=\ln|x|+x+C`

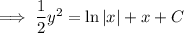
Find the value of C using the given values of x and y:

when x = 1, y = -2

`\implies (1)/(2)(-2)^2=\ln|1|+1+C`

`\implies 2=0+1+C`

`\implies C=1`

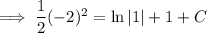
Substitute the found value of C:

`\implies (1)/(2)y^2=\ln|x|+x+1`