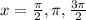Question

Find all solutions of the equation in the interval [0, 2pi).

sinx = 1 - cosx

Write your answer(s) in radians in terms of t.
If there is more than one solution, separate them with commas.

Answer 1

Explanation:

Begin by squaring both sides to get rid of the radical. Doing that gives you:

`sin^2x=1-cosx`

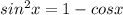
Now use the Pythagorean identity that says

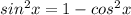`sin^2x =1-cos^2x` and make the replacement:

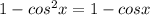`1-cos^2x=1-cosx`. Now move everything over to one side of the equals sign and set it equal to 0 so you can factor:

`1-cos^2x+cosx-1=0` and then simplify to

`cosx-cos^2x=0`

Factor out the common cos(x) to get

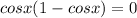`cosx(1-cosx)=0` and there you have your 2 trig equations:

cos(x) = 0 and 1 - cos(x) = 0

The first one is easy enough to solve. Look on the unit circle and see where, one time around, where the cos of an angle is equal to 0. That occurs at

`x=(\pi )/(2),(3\pi)/(2)`

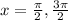
The second equation simplifies to

cos(x) = 1

Again, look to the unit circle and find where the cos of an angle is equal to 1. That occurs at π only.

So, in the end, your 3 solutions are

`x=(\pi)/(2),\pi,(3\pi)/(2)`