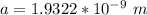Answer:
Generally the barrier width is
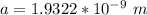
Explanation:
From the question we are told that
The tunneling probability required is

The barrier height is
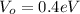
The electron energy is
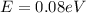
Generally the wave number is mathematically represented as
![k = \sqrt{ (2 * m [V_o - E])/(\= h^2) }](https://img.qammunity.org/2021/formulas/mathematics/high-school/kirdy8jhcmfetsag65z5ekbdyg5ucgz5cf.png)
Here m is the mass of the electron with the value

h is is know as h-bar and the value is
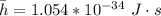
So
![k = \sqrt{ (2 * 9.11 *10^(-31 ) [0.4 - 0.04] * 1.6*10^(-19))/([1.054*10^(-34)^2]) }](https://img.qammunity.org/2021/formulas/mathematics/high-school/lmjvau6mscuu9uq4o5lewa3aoqebvx2abs.png)
=>
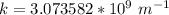
Generally the tunneling probability is mathematically represented as
![T = 16 * (E)/(V_o ) * [1 - (E)/(V_o) ] * e^(-2 * k * a)](https://img.qammunity.org/2021/formulas/mathematics/high-school/ec1mh9n7c9xtm3cgdzfdgmjexxs0dxg8t4.png)
So
![1.0 *10^(-5) = 16 * (0.04)/(0.4 ) * [1 - (0.04)/(0.4) ] * e^{-2 * 3.0736 *10^(9) * a}](https://img.qammunity.org/2021/formulas/mathematics/high-school/hsvoz8kt107ujaloscictl59lr0h0t46ap.png)
=>
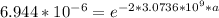
Taking natural log of both sides
![ln[6.944*10^(-6)] = -2 * 3.0736 *10^(9) * a}](https://img.qammunity.org/2021/formulas/mathematics/high-school/qrhj1pnvw76iv1j94zzm5gq509unrtvdj3.png)
=>
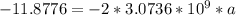
=>