-------------------------------------------------------------------------------------------------------------
Answer:
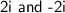
-------------------------------------------------------------------------------------------------------------
Given:
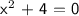
Find:

Solution: In order to find the value of x we must isolate x by itself and it will produce the result. In this case we need to subtract 4 from both sides and square root both sides in order to isolate x.
Subtract 4 from both sides
Square root both sides
After completing all of the step we are able to determine that x is equal to both 2i and -2i.