Answer:
The first term of the sequence is 512 or -512
Explanation:
Geometric Progression
The general term n of a geometric progression of first term a1 and common ratio r is:
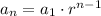
We are given:
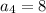
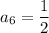
Applying the equation for n=4:
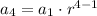
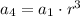
We have:
![a_1\cdot r^(3)=8\qquad\qquad[1]](https://img.qammunity.org/2021/formulas/mathematics/college/81izroya9zt79b1w9r9hhyah3u9oeztbbs.png)
Applying the equation for n=6:
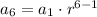
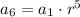
We have:
![\displaystyle a_1\cdot r^(5)=(1)/(2) \qquad\qquad[2]](https://img.qammunity.org/2021/formulas/mathematics/college/7gvea0b4hhwka4mnyzkywrt750eko37fys.png)
Dividing [2] by [1]:
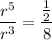
Operating:
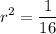
Taking the square root:
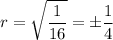
There are two possible solutions:
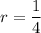
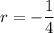
From [1]:
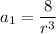
This gives also two possibles solutions for a1:
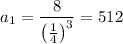
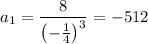
Thus, the first term of the sequence is 512 or -512