Question

If the fourth and the sixth terms of a geometric progression are 8 and 1/2 respectively, then the first

term of this sequence will be;​

Answer 1

The first term of the sequence is 512 or -512

Explanation:

Geometric Progression

The general term n of a geometric progression of first term a1 and common ratio r is:

`a_n =a_1\cdot r^(n-1)`

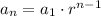
We are given:

`a_4=8`

`\displaystyle a_6=(1)/(2)`

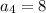
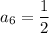
Applying the equation for n=4:

`a_4 =a_1\cdot r^(4-1)`

`a_4 =a_1\cdot r^(3)`

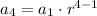
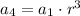
We have:

`a_1\cdot r^(3)=8\qquad\qquad[1]`

Applying the equation for n=6:

`a_6 =a_1\cdot r^(6-1)`

`a_6 =a_1\cdot r^(5)`

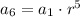
We have:

`\displaystyle a_1\cdot r^(5)=(1)/(2) \qquad\qquad[2]`

Dividing [2] by [1]:

`\displaystyle (r^(5))/(r^(3))=((1)/(2))/(8)`

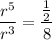
Operating:

`\displaystyle r^(2)=(1)/(16)`

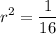
Taking the square root:

`\displaystyle r=\sqrt{(1)/(16)}=\pm (1)/(4)`

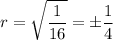
There are two possible solutions:

`\displaystyle r=(1)/(4)`

`\displaystyle r=-(1)/(4)`

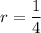
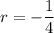
From [1]:

`\displaystyle a_1 =(8)/(r^(3))`

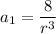
This gives also two possibles solutions for a1:

`\displaystyle a_1 =(8)/(\left((1)/(4)\right)^(3)) =512`

`\displaystyle a_1 =(8)/(\left(-(1)/(4)\right)^(3)) =-512`

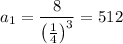
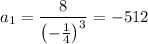
Thus, the first term of the sequence is 512 or -512