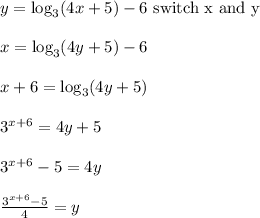Answer:
f inverse of x is equal to 3 to the power of the quantity x plus 6 end quantity minus 5 all over 4
Explanation:
The function
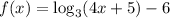 can be thought of as a series of steps, one operation at a time:
can be thought of as a series of steps, one operation at a time:
Start with x
Multiply by 4
Add 5
Take the
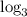
Subtract 6
That gives you a function value
 .
.
To get the inverse function, read that list from the bottom up (in reverse order, using inverse operations at each step).
Start with x (a bit confusing, because this x represents the function value you get at the end of the above list).
Add 6 (add is the inverse operation of subtract)
Raise 3 to the ...
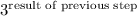
Subtract 5
Divide by 4

Let's test this out. Find f(1).

Now put -4 into the inverse function.
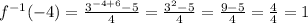
The final result is the number we started with when we put 1 into f(x).
Finding an inverse is reversing the action of the function f by doing inverse operations in "backwards" order.
A lot of authors have you do this by switching x and y in the formula for a function, then solving for x.