Answer:
No Real Roots
Explanation:
Hello!
To determine the types of roots a quadratic has, we can use the Discriminant.
Refer to the quadratic formula:
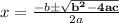
The bolded part (b² - 4ac) is the Discriminant.
Determining the roots
- Positive Discriminant gives us 2 roots that are real (can be rational or irrational)
- Zero Discriminant gives us 1 root that is real and rational (can also be known as a double root)
- Negative Discriminant gives us 2 roots that are not real, or imaginary.
We can plug in our values from the quadratic into the Discriminant Formula b² - 4ac.
Solve
Since the discriminant is negative, there are two imaginary roots, or roots that don't exist.
The are no real roots for this quadratic.