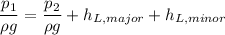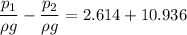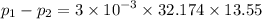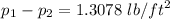Question

An exhaust system is modeled as 9 ft of 0.125 ft diameter smooth pipe with the equivalent of (7) 90○ elbows and a muffler. The muffler has a measured loss coefficient of 8.5. The average flowrate is 0.1 ft3 /s with a fluid density of 0.003 slug/ft3 and a dynamic viscosity of 4.7 ⋅ 10−7 lbf-s/ft2 . (a) Determine the system resistance. (b) Compute the pressure drop through the exhaust system.

Answer 1

The velocity of the exhaust air flow using continuity equation

`$V=(Q)/((\pi)/(4)d^2)$`

`$V=(0.1)/((\pi)/(4)(0.125)^2)$`

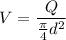
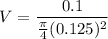
= 8.148 ft/s

Reynolds number,

`$Re=(\rho V d)/(\mu)$`

`$Re=(3* 10^(-3)* 8.148* 0.125)/(4.7* 10^(-7))$`

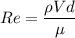
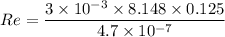
= 6501.06

As Re > 4000, the flow is turbulent.

Now calculating the friction factor of the flow,

`$f=(0.316)/((Re)^(0.25))$`

`$f=(0.316)/((6501.06)^(0.25))$`

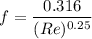
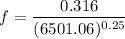
= 0.03519

Calculating the major head loss in the pipe

`$h_(L,major)=(flV^2)/(2gd)$`

`$h_(L,major)=(0.03519* 9* (8.148)^2)/(2* 32.174* 0.125)$`

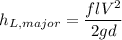
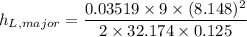
= 2.614 ft

Calculating the minor head loss in the pipe

`$h_L=n\left((k_(L,elbow) V^2)/(2g)\right)+(k_(L,muffler)V^2)/(2g)$`

`$h_L=(V^2)/(2g)\left(nk_(L,elbow)+k_(L,muffler\right))$`

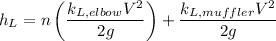
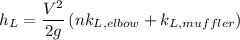
Here, n = number of elbows.

`$h_(L,minor)=((8.148)^2)/(2* 32.174)\left(7* 0.3+8.5)}$`

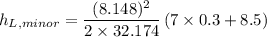
= 10.936 ft

Now using Bernoulli equation between the entrance of the pipe and the exit of the pipe

`$(p_1)/(\rho g)+(V_1^2)/(2g)+z_1=(p_2)/(\rho g)+(V_2^2)/(2g)+z_2\\h_(L,major)+h_(L,minor)$`

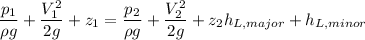
Substitute
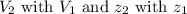`$V_2 \text{ with}\ V_1 \text{ and}\ z_2 \text{ with}\ z_1$`, we get

`$(p_1)/(\rho g)=(p_2)/(\rho g)+h_(L,major)+h_(L, minor)$`

`$(p_1)/(\rho g)-(p_2)/(\rho g)=2.614+10.936$`

`$p_1-p_2=3* 10^(-3)* 32.174 * 13.55$`

`$p_1-p_2=1.3078 \ lb/ft^2$`