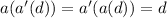Answer:
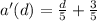
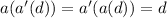
Explanation:
Given
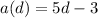
Solving (a): Write as inverse function
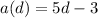
Represent a(d) as y
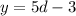
Swap positions of d and y
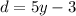
Make y the subject
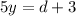
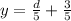
Replace y with a'(d)
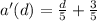
Prove that a(d) and a'(d) are inverse functions
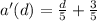 and
and
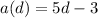
To do this, we prove that:
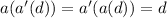
Solving for
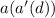
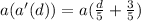
Substitute
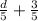 for d in
for d in
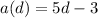
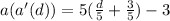
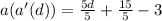
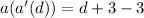
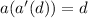
Solving for:
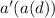
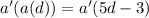
Substitute 5d - 3 for d in
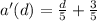
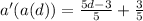
Add fractions
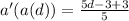
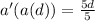
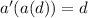
Hence: